Hoy lo que vamos a hacer es DIVERTIRNOS con acertijos de billar. Voy a poner un recopilatorio de ejercicios en los que el billar es el protagonista. Pongo los ejercicios y al final pongo la solución por orden de cada uno. No seáis ansiosos y bajéis al pie de página muy rápido.
Vamos allá:
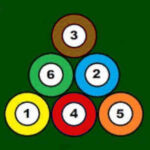
1- Selecciona tres bolas de billar que sumen 30:
Este ejercicio si eres billarista no lo puedes fallar. Se observador y piénsalo bien. El juego tiene solución 😉
2- En una mesa de billar hay dos bolas A y B:
Vamos con un ejercicio famoso que si eres billarista aprenderás una regla de nivel avanzado que probablemente ni que seas un gran jugador sabrás… pero AVISO, se requiere un poco de conocimientos de matemáticas, si no sabes y quieres aprender te lo explico, y si sabes y te quieres probar te animo a hacerlo. La solución y explicación esta abajo. Si lo ves muy difícil pasa al siguiente. Y si te gusta el billar lee el final, aunque no te salga el cálculo.
3- A ver si consigues con 6 bolas de billar formar tres filas de tres bolas y encima que todas las filas sumen 10.
4- En un arreglo de seis bolas de billar ¿cuántos grupos de tres bolas se pueden formar
Este problema requiere conocimientos de estadística, en concreto combinaciones. A diferencia del ejercicio número 2 donde se pueden sacar conclusiones interesantes en billar, en este último solo te divertirás si te gustan las matemáticas. O si no te gustan pero el profe te puso un ejercicio similar 🙂 La solución al final.
1- SOLUCIÓN
A que no te has dado cuenta que la bola 9 debería ser blanca y rayada de color amarillo, ¡¡si eres jugador no puedes fallar esto!!
Pues si, no es una bola 9, sino una 6 que se ha dado la vuelta, habrá salido rodando…
el caso es que como en principio todas las bolas eran impares, al sumar tres bolas, siempre iba a dar impar, pero si hay una bola 6 la cosa cambia.
La 6 + 11 + 13 suman 30.
2- SOLUCIÓN
El problema se podía resolver con el teorema del coseno, pero para hacerlo sencillo usaremos la ecuación del movimiento rectilíneo uniformemente variado (MURV) y el teorema de pitágoras.
Hay que imaginar el punto inicial de las bolas como el vértice de un triángulo. Y la distancia que recorre cada una de las bolas serán los lados que salen de ese vértice inicial.
Si tenemos en cuenta esto nos daremos cuenta que solo nos hará falta saber la última banda para resolver el ejercicio.
Vamos a descubrir la longitud de los dos lados que salen del vértice inicial:
MURV:
X = Xo + Vo*t + a*t²/2
X es la posición final. Que es lo que buscamos.
Xo es la posición inicial. Que en nuestro caso será 0 en las dos bolas.
Vo es la velocidad inicial. Que también será 0 en las dos bolas, ya que empiezan paradas.
a es la aceleración, que será de 12 en una bola y 24 en la otra.
t es el tiempo. Que será 1 segundo.
X = 0 + 0*1 + 12*1²/2
0 por 1 es 0 así que tenemos que 0+0 es 0. Solo hace falta calcular el final de la fórmula.
12*1²/2
1 al cuadrado es 1 por 1, es decir 1.
12*1/2
Aquí hay que saber multiplicar un número por una fracción. Se multiplica 12 * 1 y se divide entre el denominador (2). Sale 6.
Para la bola A:
Xo = 0 cm
Vo = 0 cm/s
t = 1 s
a = 12 cm/s²
X = 0 + 0*1 + 12*1²/2 = 6 cm
Para la bola B:
Xo = 0 cm
Vo = 0 cm/s
t = 1 s
a = 24 cm/s²
X = 0 + 0*1 + 24*1²/2 = 12 cm
Ahora se aplica el teorema de Pitágoras ya que ya sabemos la longitud de los triángulos.
c = 12 cm
a = 6 cm
12 = √ 6² + b²
b = √ 12² – 6²
b = √144 – 36
b = √108 = 6√3 cm
Si no entendéis este último paso, lo que hace es substituir 108 por 36*3. Se hace esto por simplificar el resultado, ya que 36 es igual a 6² y puede salir de la raíz quitándole el cuadrado (porque la raíz es cuadrada).
3- SOLUCIÓN
Son COMBINACIONES DE 6 ELEMENTOS TOMADOS DE 3 EN 3. Si sabes de esto es un ejercicio fácil.
Existen fórmulas de combinatoria para calcularlo.
C (m,n) = m! / n! (m-n)! =
C (6,3) = 6! / 3!·(6-3)! = (6×5×4×3×2) / 3×2×3×2 = 720 / 36 = 20 grupos distintos.
4- SOLUCIÓN
Hay que ponerlas en triángulo de esta forma se consigue tres filas con 6 bolas que tal vez es lo más difícil de todo y con la siguiente colocación de los números:
